
|
หน้าแรก |
คลังข้อสอบ |
O-NET |
สสวท. |
เพชรยอดมงกุฏ |
สอบเข้าม.1 |
สอบเข้าม.4 |
|
Reading |
Listening |
สมุดจดศัพท์ |
เกมคำศัพท์ |
คณิตศาสตร์ |
E-BOOK |
ผู้ทำเว็บ |
 |
MONEY SUMMARY สรุปเรื่องเงินให้เข้าใจง่ายใน 1 เล่ม รวบพื้นฐานความเข้าใจทางการเงินอย่างรอบด้านที่ทุกคนควรรู้ เหมาะกับผู้มีรายได้ทุกคนที่อยากเริ่มต้นศึกษาด้วยตัวเอง |
เตรียมตัวสอบคณิตศาสตร์
O-NET คือการสอบเพื่อวัดผลการศึกษาขั้นพื้นฐาน ข้อสอบ O-NET เป็นข้อสอบเพื่อทดสอบความรู้พื้นฐาน ไม่ใช่ข้อสอบที่ใช้สอบแข่งขัน
ฉะนั้นระดับความยากจึงน้อยกว่าข้อสอบแข่งขันที่ใช้คัดเลือกนักเรียนเข้ามหาวิทยาลัย
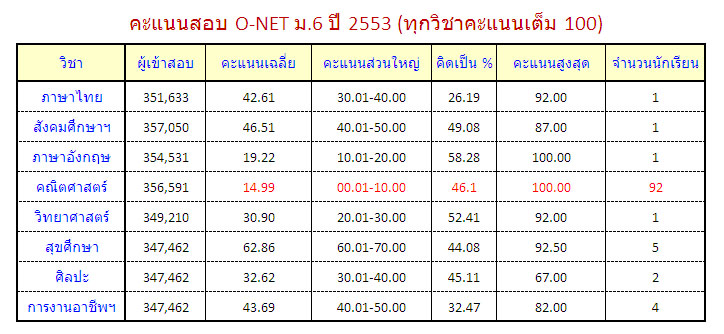
ข้อสอบยากเกินไป ?
...ไม่น่าใช่... เพราะมีนักเรียนได้คะแนน เต็ม 100 คะแนน ถึง 92 คน เป็นวิชาที่มีนักเรียนสอบได้คะแนนเต็มมากที่สุด ขณะเดียวกันก็เป็นวิชาที่มีนักเรียนได้คะแนนต่ำสุดมากที่สุดด้วย เป็นวิชาเดียวที่คะแนนสูงสุดและต่ำสุดต่างกันมากราวฟ้ากับเหว
เกิดอะไรขึ้นกับการสอบวิชาคณิตศาสตร์ ?
ถ้าคุณเข้าใจวิธีเตรียมตัวสอบคณิตศาสตร์ คุณจะไม่แปลกใจที่คะแนนสอบออกมาในลักษณะนี้
การเตรียมตัวสอบคณิตศาสตร์ต้องเตรียม 2 ส่วน
ส่วนที่ 1 เป็นภาคทฤษฏี คือเข้าใจเนื้อหาในตำราเรียน
ส่วนที่ 2 เป็นภาคปฏิบัติคือฝึกทำข้อสอบเก่า (ข้อสอบของปีที่ผ่าน ๆ มา)
'การเข้าใจเนื้อหาในตำราเรียน' กับ 'การทำข้อสอบได้' เป็นคนละเรื่องกัน
'ไม่จริงมั๊ง ถ้าเข้าใจก็จะทำข้อสอบได้ ถ้าทำข้อสอบไม่ได้คือไม่เข้าใจ มันเรื่องเดียวกันนะ '
 |
ขอเปรียบเทียบ 'การเตรียมตัวสอบคณิตศาสตร์' กับ 'การขี่จักรยาน' เพื่อให้เห็นภาพชัดเจน การรู้วิธีขี่จักรยานคือภาคทฤษฏีที่ต้องเข้าใจก่อนว่าการขี่จักรยานทำอย่างไร ภาคปฏิบัติคือหัดขี่ รู้วิธีขี่จักรยานแต่ไม่หัดขี่ ความรู้ที่มีอยู่ก็ไม่มีประโยชน์เพราะขี่ไม่เป็น |
โดยให้จักรยาน 1 คัน (ข้อสอบ 1 ชุด) แล้วให้นักเรียนขี่ให้ดู (นักเรียนทำข้อสอบ)
ถ้าถามนักเรียนว่าวิธีขี่จักรยานทำอย่างไร (ภาคทฤษฏี) นักเรียนทุกคนตอบได้ว่า
วิธีขี่จักรยานมี 3 ขั้นตอนคือ
1) ใช้มือสองข้างจับแฮนจักรยาน
2) นั่งคร่อมจักรยานบนอาน
3) ใช้ขา 2 ข้างปั่นให้จักรยานเคลื่อนไปข้างหน้า
นักเรียนทุกคนรู้วิธีขี่จักรยาน แต่ไม่ใช่ว่านักเรียนทุกคนขี่จักรยานเป็น แม้จะบอกวิธีขี่จักรยานได้ถูกต้อง (เข้าใจภาคทฤษฏี) แต่ถ้าขี่ไม่ได้ ก็สอบไม่ผ่าน เช่นเดียวกับที่นักเรียนเข้าใจเนื้อหาคณิตศาสตร์ในตำราเรียน (เข้าใจภาคทฤษฏี) แต่ถ้าทำข้อสอบไม่ได้ (ปฏิบัติไม่ได้) ก็สอบไม่ผ่าน
การสอนนักเรียนขี่จักรยานไม่ได้สอนทีละคน แต่เป็นการสอนนักเรียนทั้งห้อง และสอนหลายห้อง ครูจึงเริ่มจากภาคทฤษฏีในห้องเรียนคือ อธิบายวิธีขี่จักรยาน และสาธิตการขี่จักรยานให้ดู เมื่อนักเรียนเข้าใจแล้ว ต้องไปฝึกกันเองนอกห้องเรียน ครูมีบทบาทเฉพาะในส่วนที่เป็นภาคทฤษฏี ทำหน้าที่สอนให้นักเรียนเข้าใจภาคทฤษฏี ส่วนภาคปฏิบัติเป็นความรับผิดชอบของนักเรียนที่ต้องหาเวลาไปฝึกกันเอง ครูไม่สามารถตามไปดูว่านักเรียนแต่ละคนขยันฝึกกันแค่ไหน แต่จะนัดวันมาสอบ คนที่ขยันฝึกก็จะขี่จักรยานได้ สอบผ่าน คนที่ไม่ยอมฝึกหรือฝึกน้อยเกินไป ก็จะขี่จักรยานไม่ได้ สอบไม่ผ่าน
การสอนคณิตศาสตร์ก็เช่นกัน เริ่มจากครูอธิบายเนื้อหาภาคทฤษฏีให้ฟัง แล้วทำโจทย์ตัวอย่างให้ดูบนกระดาน เหมือนสาธิตการขี่จักรยานให้ดู เมื่อนักเรียนเข้าใจแล้ว ต้องไปฝึกภาคปฏิบัติกันเองที่บ้าน (ทำการบ้าน ฝึกทำข้อสอบเก่า) จากนั้นนัดวันมาสอบ ถ้านักเรียนไม่ฝึกภาคปฏิบัติ ก็จะสอบไม่ผ่าน เพราะข้อสอบเป็นการทดสอบภาคปฏิบัติ ไม่ใช่ภาคทฤษฏี โจทย์ไม่ได้ถามว่า
..... คืออะไร ? หรือ
..... เป็นอย่างไร ?
แต่โจทย์ให้ปัญหามา ต้องวิเคราะห์แล้วคำนวณว่าได้เท่าไร ?
นักเรียนที่ตอบได้คือคนที่เข้าใจภาคทฤษฏี และสามารถนำความเข้าใจนั้นมาปฏิบัติได้จริง จึงจะได้คำตอบ
สาเหตุที่นักเรียนส่วนใหญ่ทำข้อสอบไม่ได้ เพราะละเลยภาคปฏิบัติ พวกเขาเตรียมตัวสอบคณิตศาสตร์แบบเดียวกับเตรียมตัวสอบวิชาสังคมฯ คืออ่านหนังสือ เข้าใจเนื้อหาในหนังสือ แล้วเข้าห้องสอบ โดยไม่ฝึกภาคปฏิบัติ ภาคปฏิบัติคือส่วนที่มีบทบาทสำคัญต่อคะแนนสอบ ไม่ใช่ภาคทฤษฏี
นักเรียนส่วนใหญ่มีทัศนคติว่า การทำข้อสอบคณิตศาสตร์ยากกว่าการทำข้อสอบสังคมฯ เป็นเพราะการเตรียมตัวสอบคณิตศาสตร์ มีทั้งภาคทฤษฏีและภาคปฏิบัติ ในขณะที่การเตรียมตัวสอบสังคมฯ มีเพียงภาคทฤษฏี แต่คะแนนสอบ O-NET ปี 2553 แสดงให้เห็นว่า การทำคะแนนสูงสุดในวิชาคณิตศาสตร์นั้นทำได้ง่ายกว่า นักเรียนที่เข้าสอบวิชาสังคมศึกษาฯ มีมากกว่านักเรียนที่เข้าสอบวิชาคณิตศาสตร์ แต่ไม่มีใครได้คะแนนเต็มในวิชาสังคมศึกษาฯเลย ในขณะที่มีนักเรียนได้คะแนนเต็มในวิชาคณิตศาสตร์ถึง 92 คน ตัวเลขนี้ทำให้สงสัยว่าวิชาสังคมฯง่ายกว่าวิชาคณิตศาสตร์จริงหรือ ?
คำตอบของข้อสอบคณิตศาสตร์มีมาตรฐานเดียว ทุกอย่างชัดเจน พิสูจน์ได้ว่าถูกหรือผิด ต่างจากคำตอบของข้อสอบวิชาสังคมฯ ซึ่งส่วนหนึ่งอิงกับความคิดเห็นของแต่ละคนที่อาจคิดแตกต่างกัน ยากที่จะพิสูจน์ว่า ความคิดเห็นของใครถูก ของใครผิด ดังนั้นจึงเกิดข้อโต้แย้งในคำตอบได้เสมอ
ในชีวิตประจำวัน มีน้อยเรื่องที่ทุกคนมีความคิดเห็นตรงกันเป็นเอกฉันท์ จึงเป็นเรื่องยากทางสังคมที่จะกำหนดให้มีมาตรฐานเดียว สังคมรอบตัวเรามีหลายมาตรฐานอยู่ตลอดเวลา ทั้งนี้เพราะแต่ละคนคิดต่างกัน และพยายามใช้ความคิดของตนเองกำหนดมาตรฐาน จึงเกิดมาตรฐานมากมายตามความคิดของผู้มีอำนาจในสังคม
ในวิชาคณิตศาสตร์ทุกอย่างมีมาตรฐานเดียว โจทย์ข้อสอบหนึ่งข้อมีวิธีทำได้หลายวิธี แต่ทุกวิธีอยู่บนมาตรฐานเดียวกัน คือได้คำตอบเท่ากัน ทุกคนจึงยอมรับวิธีทำที่แตกต่างได้ เพราะผลสุดท้ายจะจบที่จุดหมายเดียวกัน นี่เป็นเหตุผลที่สามารถทำคะแนนเต็มในวิชาคณิตศาสตร์ได้ไม่ยาก แต่ที่นักเรียนส่วนใหญ่รู้สึกว่า ข้อสอบคณิตศาสตร์ยาก เพราะพวกเขาฝึกภาคปฏิบัติน้อยเกินไป
ทำไมละเลยการฝึกภาคปฏิบัติ
1 ) | ไม่เข้าใจภาคทฤษฏี จึงฝึกภาคปฏิบัติไม่ได้เพราะภาคทฤษฏีเป็นพื้นฐานของภาคปฏิบัติ |
2 ) | ไม่ขยัน เข้าใจภาคทฤษฏี รู้ว่าการฝึกทำข้อสอบเก่าช่วยให้สอบได้คะแนนดี แต่ขี้เกียจฝึก |
3 ) | เชื่อว่าสามารถทำข้อสอบได้โดยไม่ต้องฝึกทำข้อสอบเก่า |
ความเชื่อที่ว่า 'สามารถทำข้อสอบได้โดยไม่ต้องฝึกทำข้อสอบเก่า'
เป็นอีกสิ่งที่นักเรียนหลายคนพลาด ทำไมนักเรียนจึงเชื่อเช่นนั้น ?
นักเรียนจำนวนมากเตรียมตัวสอบคณิตศาสตร์ด้วยการอ่านโจทย์ข้อสอบเก่าแล้วพลิกดูเฉลย หรือดูติวเตอร์เฉลยข้อสอบในโรงเรียนกวดวิชา โดยไม่ได้ฝึกทำข้อสอบด้วยตัวเอง ถ้าเข้าใจภาคทฤษฏี จะดูเฉลยรู้เรื่อง และดูเป็นเรื่องง่าย ๆ เมื่อดูเฉลยไปมาก ๆ จะเกิดความมั่นใจว่าตัวเองสามารถทำได้ ทั้งที่ยังไม่เคยลงมือทำด้วยตัวเองเลย การดูเฉลยข้อสอบโดยไม่ฝึกทำข้อสอบด้วยตัวเอง คือการดูคนอื่นขี่จักรยาน ต่อให้ดูครบ 100 ครั้ง ก็ไม่ช่วยให้ตัวเองขี่จักรยานได้
ถ้าต้องการขี่จักรยานเป็น ต้องขึ้นไปขี่จักรยานด้วยตัวเอง แล้วจะพบความจริงว่า การทรงตัวบนจักรยาน 2 ล้อนั้นไม่ง่ายเหมือนดูคนอื่นขี่ นักเรียนที่ดูแต่เฉลยโดยไม่ได้ฝึกทำด้วยตัวเอง เมื่อลงมือทำข้อสอบจริงครั้งแรกในห้องสอบ จะงง เริ่มต้นไม่ถูก ไม่รู้ว่าจะเริ่มจากจุดไหนก่อน เมื่อทำแล้วติดปัญหา ก็ไม่รู้จะแก้ปัญหาอย่างไร ทำต่อไม่ได้ ผลสุดท้ายก็ไม่ได้คะแนน ฝีมือขี่จักรยานของเด็กกลุ่มนี้จะขี่ส่ายไปมาเหมือนงูเลื้อย ผลสุดท้ายไม่สามารถขี่ไปถึงปลายทาง เป็นกลุ่มที่น่าเสียดาย เพราะเข้าใจภาคทฤษฏีแล้ว อุตส่าห์ขยันเตรียมตัวสอบ แต่ เตรียมตัวสอบคณิตศาสตร์ผิดวิธี
จากผลสอบ O-NET ข้างต้น กลุ่มที่ได้คะแนนไม่เกิน 10 คะแนน ที่มีนักเรียนถึง 46.1%
อาจมีนักเรียนกลุ่มนี้อยู่ด้วย
ภาคทฤษฏีใช้เวลาน้อย ภาคปฏิบัติใช้เวลามาก
การเข้าใจวิธีขี่จักรยาน(ภาคทฤษฏี) ใช้เวลาไม่ถึง 1 นาที แต่การฝึกขี่จักรยาน (ภาคปฏิบัติ) ให้คล่องเพื่อให้สามารถขี่ไปได้ทุกหนทุกแห่งต้องใช้เวลาเป็นเดือน เพราะสภาพเส้นทางในแต่ละสถานที่ต่างกันจึงต้องการทักษะที่ต่างกัน แต่ทุกเส้นทางใช้ทฤษฏี (วิธีขี่จักรยาน) เดียวกัน ขอยกตัวอย่างเปรียบเทียบให้เห็นชัดเจน
การแยกตัวประกอบพีชคณิต เป็นความรู้พื้นฐานที่ใช้ในการแก้สมการกำลังสอง และกำลังสาม การนำความเข้าใจนี้ไปแก้สมการ ในภาคปฏิบัติ จะพบสมการหลากหลายที่มีความยากง่ายต่างกัน เหมือนการขี่จักรยานไปในสถานที่ต่าง ๆ
 |
เริ่มจากสมการที่มีตัวเลขน้อยๆ ไม่ซับซ้อน เปรียบเหมือนขี่จักรยานบนถนนคอนกรีตเรียบๆ กว้างๆ ขี่ง่ายๆ ไม่ต้องใช้ทักษะมาก ตัวอย่างโจทย์ในระดับนี้
|
 |
สมการที่มีตัวเลขมาก เป็นการเพิ่มความยากขึ้นมาอีก 1 ระดับ เปรียบเทียบกับการขี่จักรยานบนสะพานไม้ พื้นไม่เรียบ ต้องการทักษะการขี่สูงขึ้นอีก 1 ระดับ ตัวอย่างโจทย์ในระดับนี้
|
 |
วิธีแยกตัวประกอบใช้ได้กับการแก้สมการกำลังสาม แต่ต้องการทักษะการแยกตัวประกอบอีกระดับหนึ่ง เปรียบเทียบกับการขี่จักรยานผ่านสะพานแคบ ต้องการทักษะมากกว่าการขี่จักรยานผ่านสะพานกว้าง ตัวอย่างโจทย์ในระดับนี้
|
 |
สำหรับสมการที่มีตัวเลขซับซ้อน ต้องการทักษะการแยกตัวประกอบที่ผ่านการฝึกฝนมาอย่างดี เปรียบเทียบกับการขี่จักรยานผ่านสะพานแคบที่ไม่มีราวสะพาน ต้องการทั้งทักษะการขี่และความมั่นใจในฝีมือของตัวเอง ตัวอย่างโจทย์ในระดับนี้
|
การขี่จักรยานผ่าน 4 เส้นทางนี้ใช้วิธีเดียวกัน แต่ต้องการทักษะที่ต่างกัน เช่นเดียวกับการหาคำตอบของสมการ 4 สมการนี้ ใช้วิธีแยกตัวประกอบ แต่ไม่ได้หมายความว่านักเรียนที่เข้าใจวิธีแยกตัวประกอบแล้ว จะหาคำตอบของ 4 สมการนี้ได้ หาคำตอบได้หรือไม่ ขึ้นกับทักษะของแต่ละคนว่าผ่านการฝึกฝนมามากน้อยแค่ไหน ?
ระดับมาตรฐานของการขี่จักรยานคือสามารถขี่จักรยานให้เคลื่อนที่ไปเป็นเส้นตรง ดังนั้นคนที่ฝีมือถึงระดับมาตรฐานแล้วจะขี่ผ่านสะพานแคบ ไม่มีราว ได้ แต่คนที่ขี่จักรยานส่ายเป็นงูเลื้อยจะตกสะพาน ด่านนี้เป็นการคัดผู้ที่ฝีมือไม่ได้มาตรฐานออก
นักเรียนที่ผลสอบ O-NET อยู่ในกลุ่ม 0 - 10 คะแนน ซึ่งมีอยู่ 46.1% คือกลุ่มที่ไม่สามารถขี่ผ่านสะพานนี้ นักเรียนกลุ่มนี้ต้องกลับไปฝึกขี่จักรยานใหม่ ต้องพาตัวเองให้ผ่านสะพานนี้ไปให้ได้ก่อน แล้วค่อยคิดเรื่องลงสนามแข่ง
'ถ้าขี่ผ่านสะพานนี้ได้ แสดงว่าสอบติดใช่ไหม ? '
'ยังครับ! ชัยชนะไม่ได้มาง่ายขนาดนั้น '
ขี่ผ่านสะพานนี้ได้ หมายถึงมีศักยภาพพอที่จะลงสนามแข่งกับคนอื่น ส่วนผลแข่งขันจะชนะหรือไม่เป็นอีกเรื่องหนึ่ง แต่ถ้าขี่ผ่านสะพานนี้ไม่ได้ ไม่ต้องคิดไปแข่งกับใครเลย เพราะรู้ผลล่วงหน้าว่า แพ้แน่นอน!
ฝีมือขี่จักรยานของคุณอยู่ในระดับไหน
นักเรียนจำนวนมาก ฝากความหวังในการสอบเข้าไว้กับติวเตอร์ โดยหวังว่าการเรียนกวดวิชากับติวเตอร์ที่เก่งจะช่วยให้สอบเข้าได้ ครูสอนคณิตศาสตร์หรือติวเตอร์ที่เก่งที่สุด สามารถพานักเรียนไปส่งได้แค่ครึ่งทาง พวกเขามีบทบาทเฉพาะในส่วนที่เป็นภาคทฤษฏี อีกครึ่งทางที่เหลือเป็นภาคปฏิบัติที่นักเรียนต้องเดินทางต่อด้วยตัวเอง และตรงนี้แหละเป็นตัวตัดสินว่าใครจะเดินทางไปถึงประตูมหาวิทยาลัย หรือประตูโรงเรียนที่ตัวเองอยากเข้าไปเรียน
ถ้าปีนี้คุณต้องลงสนามสอบแข่งขัน ต้องรีบถามตัวเองว่าฝีมือขี่จักรยานของตัวเองอยู่ในระดับไหน ?
 |  |  |
ระดับ 1 ขี่เป็นเส้นตรง
นักเรียนที่อยู่ในกลุ่มนี้คือเข้าใจภาคทฤษฏีแล้ว ทำโจทย์ข้อสอบได้บ้างไม่ได้บ้าง ถ้าถามว่าโจทย์ข้อนี้อยู่ในหัวข้อไหนของภาคทฤษฏี เขาตอบได้ ถามว่าเนื้อหาของหัวข้อนั้นในภาคทฤษฏีกล่าวไว้อย่างไร เขาอธิบายได้ แสดงว่าเขาไม่ได้หลงทาง เขารู้ว่าต้องเดินไปทางนี้ แต่การนำมาปฏิบัติอาจจะยังไม่ถูกต้องนัก เขาสามารถทำโจทย์จนได้คำตอบ แต่คำตอบถูกหรือไม่เป็นอีกเรื่องหนึ่ง อาจมีบางข้อที่ทำไม่ได้ แต่โดยรวมแล้วทำได้มากกว่าทำไม่ได้
ระดับ 2 ขี่ส่ายเป็นงูเลื้อย
นักเรียนที่อยู่ในกลุ่มนี้คือเข้าใจภาคทฤษฏีแล้ว แต่ยังไม่แม่น บอกได้ว่าโจทย์ข้อนี้อยู่ในหัวข้อไหนของภาคทฤษฏี แต่จำเนื้อหาในหัวข้อนั้นได้ไม่ครบ ลืมรายละเอียดบางส่วนซึ่งเป็นส่วนที่ต้องใช้ในการทำข้อสอบ จึงทำข้อสอบนั้นไม่ได้ หรือทำได้ไม่จบ คือเริ่มทำได้ แต่ทำแล้วติดปัญหา ทำต่อไม่ได้ ผลสุดท้ายไม่ได้คำตอบ
ระดับ 3 เดินจูงจักรยานดูคนอื่นขี่
นักเรียนที่อยู่ในกลุ่มนี้คือยังไม่เข้าใจภาคทฤษฏี บอกไม่ได้ว่าโจทย์ข้อนี้อยู่ในหัวข้อไหนของภาคทฤษฏี อ่านโจทย์ข้อสอบแล้วไม่รู้ว่าเป็นเรื่องอะไร ไม่รู้ว่าจะเริ่มทำข้อสอบอย่างไร จับต้นชนปลายไม่ถูก มืดแปดด้าน มองไม่เห็นทางออก
ขอให้ประเมินฝีมือของคุณตามความเป็นจริง อย่าหลอกตัวเอง ขั้นตอนนี้สำคัญต่อการเตรียมตัวสอบคณิตศาสตร์เพราะใช้เลือกวิธีฝึกใน ห้องสอบเสมือนจริง
| ห้องสอบเสมือนจริง | คลิกที่นี่เพื่อดูคู่มือการใช้ห้องสอบเสมือนจริง |
1) ห้องสำหรับเตรียมตัวสอบเข้าม. 1
2) ห้องสำหรับเตรียมตัวสอบเข้าม. 4
3) ห้องสำหรับเตรียมตัวสอบเข้ามหาวิทยาลัย
วิธีฝึกสำหรับผู้ที่อยู่ในระดับ 1 ขี่เป็นเส้นตรง
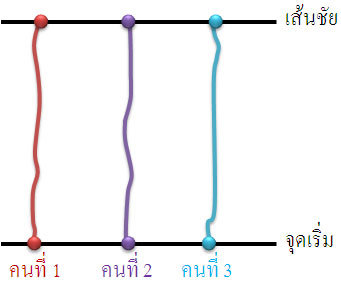 |
นักเรียนที่อยู่ในกลุ่มนี้ สามารถขี่จักรยานเป็นเส้นตรงแล้ว แต่เส้นตรงของแต่ละคนไม่เท่ากัน มีโค้งบ้าง หยักบ้าง มากน้อยต่างกัน แต่โดยรวมแล้วสามารถเดินทางออกจากจุดเริ่ม
ไปถึงเส้นชัยได้ |
ในห้องสอบมีเวลาจำกัด หากไม่สามารถทำทันทุกข้อ ต้องเลือกทำ โดยเลือกข้อที่ตัวเองมั่นใจ และใช้เวลาน้อยก่อน
วิธีฝึกสำหรับผู้ที่อยู่ในระดับ 2 ขี่ส่ายเป็นงูเลื้อย
 |
นักเรียนที่อยู่ในกลุ่มนี้ สามารถออกเดินทางจากจุดเริ่มได้ แต่หลงทิศ ไม่สามารถเดินทางไปถึงเส้นชัย แม้เข้าใจเนื้อหาที่เป็นภาคทฤษฏีแต่ไม่แม่น |
หลังจากเปิดหนังสือเรียนทบทวนเนื้อหาภาคทฤษฏีและพยายามทำข้อสอบจนถึงที่สุดแล้วยังไม่สามารถทำได้จึงดูเฉลย การดูเฉลยขอให้เป็นทางเลือกสุดท้าย เพราะเฉลยจะอธิบายทุกอย่างหมด ทำให้นักเรียนไม่ได้คิดด้วยตัวเอง นักเรียนควรพยายามคิดและวิเคราะห์ด้วยตัวเองก่อน แล้วจึงมาดูเฉลยว่าสิ่งที่ตัวเองคิดนั้นถูกหรือไม่
อย่าใช้เวลาอยู่ในระดับ 2 นาน เพราะระดับ 2 เป็นเพียงที่พักชั่วคราวสำหรับผู้ที่ยังไม่พร้อมที่จะฝึกในระดับ 1 อนุญาตให้ใช้ข้อสอบสำหรับฝึกในระดับ 2 เพียง 1 ชุด เพื่อให้เข้าใจแนวข้อสอบ จากนั้นใช้ข้อสอบและเวลาที่เหลือทั้งหมดฝึกในระดับ 1 เพราะการฝึกในระดับ 1 คือมาตรฐานการฝึกสำหรับเตรียมความพร้อมก่อนลงสนามแข่ง
วิธีฝึกสำหรับผู้ที่อยู่ในระดับ 3 เดินจูงจักรยานดูคนอื่นขี่
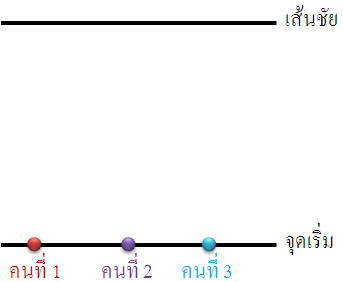 |
นักเรียนที่อยู่ในกลุ่มนี้ ไม่สามารถออกเดินทางจากจุดเริ่มได้ เมื่ออ่านโจทย์ข้อสอบแล้ว ไม่รู้ว่าจะเริ่มอย่างไร |
นักเรียนกลุ่มนี้ต้องกลับไปทบทวนเนื้อหาในหนังสือเรียน และทำแบบฝึกหัดในหนังสือก่อน แบบฝึกหัดเป็นการทดสอบความเข้าใจ จึงง่ายกว่าข้อสอบที่ใช้สอบแข่งขัน ถ้าไม่สามารถทำความเข้าใจกับเนื้อหาภาคทฤษฏีด้วยตัวเอง ต้องเรียนพิเศษหรือหาติวเตอร์มาสอน
เมื่อฝึกทำแบบฝึกหัดจนเข้าใจเนื้อหาทั้งหมดแล้ว ให้เริ่มฝึกจากระดับ 2 ความจริงถ้าเข้าใจภาคทฤษฏีอย่างถ่องแท้ สามารถข้ามไปฝึกในระดับ 1 ได้ ไม่จำเป็นต้องฝึกในระดับ 2
คุณไม่มีทางรู้ว่าคู่แข่งขันที่ลงสนามแข่งกับคุณ เขามีฝีมือแค่ไหน จนกว่าจะถึงวันประกาศผลสอบ ถึงตอนนั้นทุกอย่างสายเกินแก้ไขแล้ว ดังนั้น ถ้าต้องการคว้าชัยชนะในการแข่งขัน คุณต้องเตรียมตัวสอบคณิตศาสตร์โดยฝึกทำข้อสอบไปเรื่อย ๆ พัฒนาฝีมือขึ้นไปให้ถึงจุดสูงสุดเท่าที่ศักยภาพของคุณสามารถไปถึง
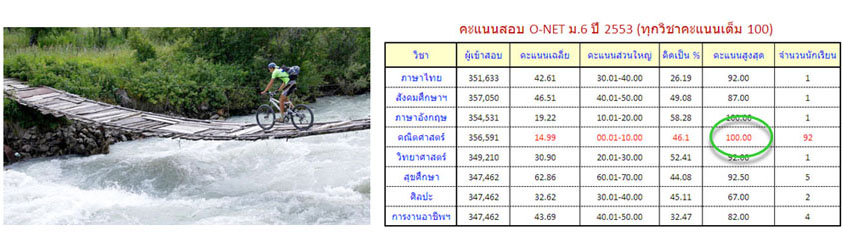
ถ้าฝึกจนฝีมือเข้าขั้นเทพขนาดนี้ ลืมคู่แข่งไปได้เลย เพราะคุณคว้าคะแนนเต็ม 100 คะแนนแน่นอน
English Voice
ฝึกฟังภาษาอังกฤษ
 |
ฝึกฟังเสียงภาษาอังกฤษด้วยเนื้อเรื่องของเทพนิยาย Beauty and the Beast
เนื้อเรื่องถูกแบ่งเป็นตอนสั้นต่อเนื่องกัน 15 ตอน แต่ละตอนเป็นแบบฝึกหัดให้นักเรียนใช้ฝึกฟังภาษาอังกฤษ
เมื่อฟังจบแต่ละตอนให้ทำแบบทดสอบ เพื่อทดสอบว่านักเรียนสามารถฟังเสียงคำศัพท์ได้มากน้อยเพียงใด
จากนั้นมีเฉลยคำตอบ และ Script พร้อมคำแปล เพื่อให้นักเรียนตรวจว่าจับใจความจากการฟังได้ครบถ้วนแค่ไหน |
สงวนลิขสิทธิ์ตามกฏหมาย Copyright (C) 2018-2024 All rights reserved.
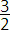
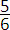
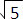 )(x +
)(x +